massa

Het gebied met negatieve massa is grijs. De uitbreiding stokt in dit gebied Bron: 1.

Negatieve massa geproduceerd

4 reacties / natuurkunde, Wetenschap / Door / 18 april 2017

Massa is altijd positief. Er zijn in de natuur geen verschijnselen bekend die een negatieve massa hebben. Althans: tot nu toe. Nu is een groep onderzoekers er voor het eerst in geslaagd om materie zich te laten gedragen als negatieve massa.

Wat is massa?

Massa lijkt een van de eenvoudigste begrippen in de natuurkunde. Schijn bedriegt hier. Hoewel Newton zijn mechanica al meer dan vier eeuwen geleden opstelde, is massa nog steeds niet geheel begrepen. Om enkele voorbeelden te geven: fotonen, lichtdeeltjes, hebben geen massa. Het is echter wél theoretisch mogelijk om licht op te sluiten in een volmaakt spiegelende bol en dan blijkt licht wel degelijk massa te hebben; het is de opsluiting van energie die massa produceert. Het meest raadselachtige aan massa is misschien wel dat het zowel traag als zwaar is, dat de verhouding traagheid/zwaarte altijd gelijk blijft. Een massa van 1 kg valt daarom even snel  als een massa van 10 kg.

Hoe gedraagt negatieve massa zich?

In theorie is het mogelijk om een minteken achter het massagetal te zetten. Je beschrijft dan negatieve massa. Op dit moment zijn er geen echte voorbeelden van negatieve massa bekend – het ‘leger dan leeg’ quantumvacuüm tussen twee platen dat het Casimireffect veroorzaakt komt er wellicht het dichtste in de buurt. Negatieve massa versnelt tegengesteld aan de richting van de versnellende kracht. Een trap tegen een bal met negatieve massa betekent dat deze jouw kant op komt vliegen. Natuurkundigen berekenden dat de ‘klassieke’ variant van negatieve massa, waarbij positieve massa alles aantrekt en negatieve massa alles afstoot, tot onzinnige uitkomsten leidde en hiermee logisch onmogelijk is. Als negatieve massa bestaat, moet deze andere negatieve massa aantrekken, maar positieve massa afstoten. Dit type is wel theoretisch mogelijk.

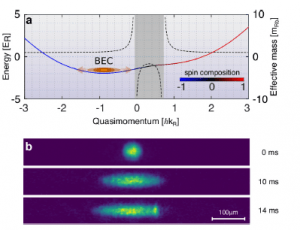
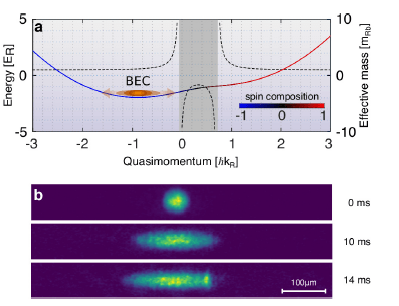
Het gebied met negatieve massa is grijs. De uitbreiding stokt in dit gebied Bron: 1.
Het gebied met negatieve massa is grijs. De uitbreiding stokt in dit gebied Bron: 1.

Bose-Einstein condensaat

Een ijzeren natuurwet is het onzekerheidsprincipe van Heisenberg. Als bijvoorbeeld de snelheid zeer nauwkeurig bekend is, wordt de positie zeer onnauwkeurig. Van een atoom in de buurt van het absolute nulpunt is de snelheid zeer nauwkeurig bekend: vrijwel nul. Dat maakt dat de positie zeer onnauwkeurig wordt: het atoom is overal tegelijk, m.a.w. verandert in een ijle waarschijnlijkheidswolk. In een Bose-Einstein condensaat overlappen de waarschijnlijkheidswolken van bosonische atomen (even aantal sub-deeltjes, zoals bij een helium-4 atoom) elkaar. Kwantummechanisch gezien is er geen onderscheid meer tussen deze atomen; ze gedragen zich als één geheel. Dit punt bereiken vereist nanokelvins, m.a.w miljardsten van graden boven het absolute nulpunt.

Hoe ontstond de negatieve massa?

Een Bose-Einstein condensaat is een extreem koud wolkje dat door middel van bijvoorbeeld lasers op zijn plaats gehouden wordt. Zo ook in dit experiment met rond de honderdduizend rubidiumatomen. Met een tweede verzameling lasers brachten de onderzoekers het condensaat in de gewenste spin- en baantoestand. Het condensaat werd in één dimensie vrijgelaten, waardoor het condensaat zich uitbreidde in deze dimensie. Hierbij ontstond er een gebied met pseudo-negatieve massa. Zodra het condensaat zich in dit gebied uitbreidde, gedroeg het zich alsof het negatieve massa had. Dat wil zeggen: het ging versnellen in de tegenovergestelde richting. Op de afbeelding is dit te zien omdat in de onderste opname de uitbreiding plotseling stopt, als door een onzichtbare kracht.

Wat is het praktische nut?

Dit is een fundamenteel-wetenschappelijke doorbraak. Als we experimenten kunnen doen met negatieve massa, al is het dan in een pseudo-vorm zoals hier, kunnen we het gedrag van het werkelijke goedje voorspellen, mochten we er in slagen deze te produceren. We kunnen nu ook gerichter zoeken naar verschijnselen waarin het mogelijk een rol speelt. Hebben we eenmaal negatieve massa verkregen, dan zouden we er bijvoorbeeld een wormgat mee open kunnen houden. Wormgaten zijn één van onze beste kanshebbers om sneller dan licht te kunnen reizen, of zelfs naar een ander universum te kunnen reizen. Dit zou het praktisch nut bijna oneindig groot maken, omdat het heelal zo eenvoudig bereisbaar voor ons wordt.

Bron
M. A. Khamehchi et al, Negative-Mass Hydrodynamics in a Spin-Orbit–coupled Bose-Einstein Condensate, Physical Review Letters (2017). DOI: 10.1103/PhysRevLett.118.155301
 (budgetoplossing)

‘Neutrino’s hebben imaginaire massa’

5 reacties / natuurkunde, Universum, Wetenschap / Door / 27 december 2014

Robert Ehrlich van de George Mason University in Virginia heeft zes waarnemingen beschreven die er op lijken te wijzen dat neutrino’s een imaginaire massa hebben, dus sneller dan het licht bewegen. Wat betekent dit precies?

Neutrino’s zijn vermoedelijk de raadselachtigste waargenomen deeltjes die we kennen. Deze ‘kleine neutraaltjes’ komen voor in drie ‘smaken’, elektron- , mu- en tauon-neutrino, waartussen ze oscilleren. Neutrino’s waarnemen is uiterst  moeilijk, omdat ze alleen via de zogeheten zwakke wisselwerking met andere deeltjes wisselwerken. Pas in de eenentwintigste eeuw is bevestigd dat ze inderdaad massa hebben, al is niet bekend welke massa. Paul Ehrlich denkt hierop een antwoord te hebben. Neutrino’s beschikken over imaginaire massa, en moeten dus tachyonen zijn, dat wil zeggen: deeltjes die alleen sneller dan de lichtsnelheid kunnen bewegen.

Imaginaire getallen
Op de middelbare school krijg je ze helaas niet, maar ze duiken op in het eerste jaar van meer exacte studies, omdat ze zo handig zijn: imaginaire getallen. Het imaginaire eenheidsgetal i is gedefinieerd als de wortel uit -1. i vermenigvuldigd met i levert dus -1 op. Herhaal je dat, dan krijg je -i. Vermenigvuldig je dit weer met i, dan kom je uit op de welbekende 1. Je hebt als het ware een rondje gemaakt rond het nulpunt van een assenstelsel, warbij de i-getallen op de y-as liggen. En inderdaad blijken imaginaire getallen alles te maken te hebben met periodieke verschijnselen.imaginary-numbers


Waarom kan je niet sneller dan het licht?
Hoe dichter je de lichtsnelheid benadert, hoe groter de totale massa wordt ten opzichte van het punt van waar je meet. De totale massa (M) is [latex]M = m/\sqrt{1 – v^2/c^2}[/latex]. Let op dat wortelteken. Als v, je snelheid, bijna even groot i als c, de lichtsnelheid, nadert v^2/c^2 1, dus de uitdrukking onder het wortelteken 1-1=0. Daardoor wordt de relativistische massa enorm. je kan dus beter snel maken dat je uit de buurt komt, als iets met relativistische snelheid op je afkomt, want al die massa wordt dan omgezet in energie. Precies de lichtsnelheid mag niet, want dan deel je door nul en zou je een oneindige massa hebben. Maar wat gebeurt er als je sneller gaat dan het licht? Dan wordt het getal onder het wortelteken negatief. Er ontstaat dan imaginaire massa. Dit, stelt Ehrlich, is er aan de hand met neutrino’s.

Zes waarnemingen
Ehrlich analyseerde de resultaten van zes eerder door anderen gedane onderzoeken en kwam tot de conclusie dat deze het beste overeenkwamen met het aannemen van een imaginaire massa. Deze onderzoeken bestudeerden CMB fluctuaties, gravitational lensing, spectra van kosmische straling, neutrino oscillaties, en neutrino dubbele beta verval. Deze middelde hij en kwam voor de rustmssa uit op een waarde van ongeveer een miljoenste van die van een elektron. Omdat in zijn theorie neutrino’s sneller dan het licht bewegen, verandert dit dus in een imaginaire massa. Hij beschrijft drie manieren hoe zijn hypothese kan worden getest: op zoek gaan naar een piek van 4.5 PeV in kosmische straling, de energieverdeling van de vrijkomende deeltjes bij het verval van de radioactieve waterstofisotoop tritium bestuderen, of afwijkingen in de neutrinoverdeling waarnemen als er in de galactische buurt een supernova met volledige instorting van de sterkern plaatsvindt. Zou zijn hypothese kloppen, en vinden we een praktische manier om met neutrino’s te communiceren op interstellaire afstanden, dan zijn de gevolgen uiteraard spectaculair. We zouden dan sneller dan licht boodschappen kunnen uitwisselen. Dat maakt een interstellaire kardashev-III beschaving veel haalbaarder.


Bron
R. Ehrlich, Six observations consistent with the electron neutrino being a tachyon with mass: m2νe = −0.11 ± 0.016eV2, Arxiv preprint server, 2014 (geaccepteerd voor publicatie door Astroparticle Physics)

De massa van individuele atomen kan nu vastgesteld worden door ze rechtstreeks te wegen.

Gevoeligste weegschaal ter wereld weegt yoctogram

2 reacties / Techniek, Wetenschap / Door / 5 april 2012

Hoe weeg je een atoomkern tot op een proton nauwkeurig? Antwoord: met een weegschaal die nauwkeurig genoeg is om de kleinst gehanteerde eenheid van massa te registreren, het yoctogram.
Individuele atomen wegen wordt nu voor het eerst in de menselijke geschiedenis mogelijk.

Hoeveel is een yoctogram?
De eenheid van massa in het Système International, het internationale standaardensysteem, is het kilogram. Eigenlijk is deze keuze verwarrend. Een duizendste deel van het kilogram is het gram. Een ton, 1000 kg, is een megagram (Mg). Kleinere gewichtseenheden dan het gram zijn, steeds in trappen van een duizendste, een milligram (een suikerkorrel), een microgram (een stofje), een nanogram (een gemiddelde lichaamscel), een picogram (de massa van het DNA in deze cel), een femtogram (de massa van een doorsnee virusdeeltje), een attogram (tien hemoglobinemoleculen), een zeptagram (een buckybal, een moleculaire voetbal van rond de zestig koolstofatomen) en tot slot het yoctogram (een proton en neutron hebben een massa van rond de 1,6 yoctogram). Een yoctogram, 10-27 kilogram, is dus extreem weinig.

De massa van individuele atomen kan nu vastgesteld worden door ze rechtstreeks te wegen.
De massa van individuele atomen kan nu vastgesteld worden door ze rechtstreeks te wegen.

Nanobuisjes
Een standaard weegschaal werkt hier allang niet meer. De kleinste gewichten worden daarom gemeten met behulp van koolstof nanobuisjes, die afhankelijk van de massa van de deeltjes die er aan kleven, met verschillende frequenties trillen. Tot nu toe slaagden onderzoekers er in met deze techniek een massa met een nauwkeurigheid van 100 yoctogram te meten – ongeveer een ijzeratoom. Om ook individuele atomen te kunnen wegen, gebruikten Adrian Bachtold en zijn collega’s van het Catalaanse Instituut voor Nanotechnologie in Barcelona korte nanobuisjes. Deze geven de nauwkeurigste resolutie en functioneren nog steeds bij de extreem lage temperaturen die nodig zijn voor deze meting.

Bij deze nauwkeurigheid zal zelfs een enkel atoom de meting ernstig verstoren. Bachtold verwijderde daarom rondzwervende atomen door tijdelijk de temperatuur van de buisjes te verhogen, zodat alle (van der Waals-)bindingen met aan de buisjes klevende atomen werden verwijderd.

Vervolgens was de sensor in staat een atoom van het edelgas xenon te wegen tot op 1,7 yoctogram nauwkeurig. Hierdoor kon het aantal deeltjes in de kern van het xenonatoom exact bepaald worden, immers protonen en neutronen hebben een massa van rond de 1,7 yoctogram. Collega-nanotechnologen, zoals Rachel McKendry van University College London, zijn zeer onder de indruk, maar noemen het goedkoop fabriceren van nanobuisjes-sensoren aan de lopende band nog een pittige technische uitdaging.

Bachtold hoopt dat de sensor kan worden gebruikt om verschillende elementen in chemische monsters vast te stellen zonder chemische reacties te gebruiken. Ook kunnen kleine verschillen in moleculaire massa een signaal zijn voor afwijkingen in de stofwisseling, dus ziekte. Een methode om individuele atomen te kunnen wegen en scheiden is ook van essentieel belang bij het winnen van grondstoffen met behulp van nanotechnologie.

Bronnen
A nanomechanical mass sensor with yoctogram resolution, Nature Nanotechnology (2012), DOI: 10.1038/NNANO.2012.42
World’s most sensitive scales detect a yoctogram, New Scientist (2012)

Het standaardkilogram vertoont een onverklaarbare gewichtsvermindering. Wat is er aan de hand?

Kilogram wijkt af

13 reacties / Wetenschap / Door / 19 november 2021

Sinds wetenschappers in het verre verleden het standaard kilogram hebben afgewogen (dat wordt gebruikt om alle andere standaarden te ijken) gebeuren er vreemde, onverklaarbare dingen mee. Zo blijkt de massa van het universele ijkkilogram in Parijs sinds 1990 met vijftig microgram te zijn gedaald. Moeten we over op een andere standaard of zijn we op het spoor van een uniek, onbekend verschijnsel?

Het standaardkilogram vertoont een onverklaarbare gewichtsvermindering. Wat is er aan de hand?Het oerkilogram

Elke weegschaal wordt geijkt met een standaardkilogram. Dat is op zijn beurt weer een kopie van de Nederlandse versie van het  ijkkilogram, die weer een kopie is van het Internationale Prototype Kilogram (IPK) dat met zes kopieën wordt bewaard in een strengbeveiligde kluis in het Franse Institut de Poids et Mésures in Sèvres, een voorstad van Parijs. Het internationale standaardkilogram is gemaakt van een legering van 90% platina met 10% iridium.  Om beschadigingen en andere veranderingen te voorkomen, staan er drie glazen stolpen over het kilogram en wordt het geregeld schoongemaakt. Om de paar decennia (de laatste keer gebeurde dit in 1990) wordt het standaardkilogram opnieuw gewogen en worden alle andere standaardkilogrammen hierop geijkt.

Raadselachtige afname in gewicht

Sinds 1890 blijkt het standaardkilogram tot vijftig microgram lichter te zijn geworden dan de kopieën van het standaardkilogram. Vijftig microgram is niet veel: een twintigmiljoenste deel van een kilo – maar dit maakt nauwkeurige natuurkundige bepalingen waarin massa een rol speelt, onbetrouwbaar. In het dagelijks leven is dit verschil verwaarloosbaar, maar niet voor wetenschappers die met zeer nauwkeurige apparatuur werken.

Meetfouten? Zou het hogere kooldioxidegehalte in de lucht (wat de lucht zwaarder maakt) door de hogere opwaartse kracht het schijnbare gewicht kleiner hebben gemaakt? Zou de oprukkende bebouwing (Sèvres is nu aan Parijs vastgegroeid) het zwaartekrachtsveld verstoren? Of is er een mysterieuze natuurkracht aan het werk? Is massa soms helemaal niet wat het lijkt, zoals schrijver dezes gelooft? De discussie is nog steeds volop aan de gang.

Vervanger voor de standaardkilo

SI, het internationale meetstelsel waarmee wetenschappers en de meeste andere mensen werken, kent zeven fundamentele eenheden. Naast de kilogram is dat de meter, de seconde, de ampère (voor stroomsterkte), de kelvin (temperatuur), de candela (lichtsterkte) en de mol (het getal van Avogadro, ongeveer het aantal waterstofatomen in een gram waterstof). Alle andere eenheden zijn hiervan afgeleid. Vroeger kenden deze andere meeteenheden ook ijkstandaarden, zo bestond er ooit een standaardmeter. Deze zijn nu alle vervangen door een definitie: in het geval van de meter bijvoorbeeld, de afstand die licht in vacuüm aflegt in 1⁄299 792 458 deel van een seconde. Dit is tot nu toe alleen nog niet gelukt met de kilogram. Uiterst vervelend, want de kilogram duikt op in de definitie van veel andere SI-eenheden. Zo wordt de ampère gedefinieerd aan de hand van de kracht die twee stroomdraden op elkaar uitoefenen en komt in de eenheid voor kracht, de newton, de kilo weer voor. Kortom: dreigt de kilo te veranderen, dan gaan de andere SI-eenheden mee.

De standaardkilogrammen bleken alle een onverklaarbare afwijking ten opzichte van elkaar te vertonen. Bron: Wikimedia Commons

Er wordt daarom gewerkt aan een vervanger voor het meer dan honderd jaar oude stuk edelmetaal. Eén strategie is het maken van een silicium bol waarvan het aantal atomen min of meer precies bekend is. En passant wordt zo ook het getal van Avogadro tot op 23 decimalen bekend. Geen triviale taak. Helaas zit je dan nog steeds vast aan een fysiek voorwerp – dat elke paar decennia moet worden vervangen. De wattbalans is daarom populairder onder metrologen (meetkundigen). In theorie moet deze extreem nauwkeurig massa’s kunnen meten en deze nauwkeurig vastnagelen aan de fundamentele constante van Planck. De praktijk blijkt echter uiterst weerbarstig. In Engeland en Duitsland wordt er gewerkt aan de wattbalans, maar toen de Engelse en Duitse wattbalans met elkaar werden vergeleken bleek er -weer- een onverklaarbaar verschil in massa te zijn van honderden microgram. Ook blijkt er een nog veel groter verschil in massa te zijn (duizend microgram) tussen beide wattbalansen en de silicium bol. Twintig keer de meetonnauwkeurigheid van het standaardkilogram. Kortom: voorlopig zijn we nog niet van de antieke platina cilinder uit Sèvres af.

Standaardkilogram nu abstract

In 2019 is het standaardkilogram niet meer in gebruik. In plaats daarvan hebben de heren en enkele dame die verantwoordelijk zijn voor het ijkkilogram, besloten over te stappen op de Constante van Planck als elementaire eenheid, en de kilogram te baseren rel;atief ten opzichte van deze eenheid. En de onverklaarbare schommelingen van de massa van de standaardkilogrammen? Deze zijn nog steeds onverklaard.

En deze afwijkingen, uitgedrukt in microgrammen, zijn nog steeds relatief enorm. Want zo kan je een tienmiljoenste verschil in massa wel noemen. De eenvoudigste verklaring zou zijn dat de standaardkilogrammen gassen uit de atmosfeer absorberen. Van metalen als palladium is bekend dat ze waterstof absorberen. Anderen vermoeden dat er mogelijk sprake was van kwikdamp uit andere instrumenten vlakbij, die de kilogrammen doet groeien. Maar mogelijk zijn er meer exotische verklaringen. Op zich is dit wel een gedegen onderzoek waard.

Bronnen
NWT Magazine
physorg.com

massa uit licht

Massa uit licht maken, hoe massaloos licht massa krijgt

26 reacties / Wetenschap / Door / 31 augustus 2021

Massa uit licht maken is makkelijker dan het lijkt. Het is dus wellicht niet een zo groot raadsel als veel natuurkundigen denken, war massa vandaan komt. Met behulp van de reactiewetten van Newton en de relativiteitstheorie (speciaal en algemeen) kom je een heel eind.

Het is nog steeds een onopgelost raadsel dat deeltjesfysici over de hele wereld tot wanhoop brengt: waar komt massa vandaan? Einstein boekte weliswaar een fundamentele doorbraak met zijn beroemde formule energie is massa maal de lichtsnelheid in het kwadraat, maar toch is nog steeds niet verklaard waar massa vandaan komt. Fotonen, bijvoorbeeld, bezitten wel energie maar geen massa. Het graviton, wat het ook is, is nog steeds compleet spoorloos. Maar misschien is er een oplossing…

Eigenschappen van massa

Massa heeft twee eigenschappen, die voor zover we weten in principe los van elkaar staan: het is traag en het is zwaar. De traagheid van  massa uit zich in de moeite die je moet doen om een brok massa in beweging te krijgen. Een rotsblok van twee kilo is twee keer zo moeilijk in beweging te krijgen (bijvoorbeeld met een snelheid van een meter per seconde omhoog te gooien) als een rotsblok van één kilo.

Als je niet op tijd maakt dat je weg komt, kom je op onzachte wijze in aanraking met een tweede eigenschap van massa: het is zwaar. Hoe meer massa, hoe sterker de zwaartekracht op het blok werkt (en hoe sterkere zwaartekracht het blok uitoefent). Op dit principe bewust de weegschaal. Een weegschaal meet niet je massa maar je gewicht: de kracht die massa uitoefent. Als je massa verdubbelt, verdubbelt je gewicht ook. Eigenlijk is dit merkwaardig. Op het eerste gezicht lijken traagheid en zwaartekracht niets met elkaar te maken te hebben. Ook Einstein waagde zich niet aan de oplossing van dit raadsel: de algemene relativiteitstheorie beschrijft slechts wat massa doet met de ruimte er omheen (en zo zwaartekracht opwekt), niet waarom massa traag is en waarom massa überhaupt de ruimte om zich heen vervormt.

Massa uit licht maken

Einstein voorspelde dat je massa kunt maken uit energie.

massa uit licht
Een van binnen volmaakt spiegelende bol kan massa uit licht maken. Bron: NARA, public domain

Kort geleden is die voorspelling ook waargemaakt, met een extreem krachtige laser waarmee elektron- positronparen zijn gemaakt. Een kilowattuur (3,6 MJ) energie staat bijvoorbeeld gelijk aan veertig miljardste gram. Een bekende techniek in deeltjesversnellers is deeltjes versnellen tot vlak bij de lichtsnelheid waardoor ze veel meer (relativistische) massa krijgen. Op die manier is er veel energie beschikbaar om bij de botsing allerlei (hopen de onderzoekers) nog onontdekte deeltjes te produceren.
Door dit te doen weten we echter nog steeds niet wat massa eigenlijk is: immers ook elektronen en positronen hebben een elementaire massa. Wat we eigenlijk willen bereiken is een systeem zonder massa, op een kunstmatige manier massa geven, m.a.w. zowel traag maken als zwaar.

Een bol gevuld met licht krijgt massa

Het meest voorkomende massaloze deeltje dat we kennen is het foton, het lichtdeeltje. Stel je laat een wolk fotonen met samen een hoeveelheid energie van duizend miljard  (1015) kilowattuur in een massaloze, volmaakt spiegelende bol heen en weer kaatsen. Wat voor proefje je ook verzint, bij elke meting lijkt het alsof de inhoud van de volmaakt spiegelende bol een massa heeft van ongeveer veertig gram.

Licht wordt traag

Wil je de bol bijvoorbeeld van je af verplaatsen, dan krijgen de fotonen die op het moment dat je tegen de bol duwt tegen de wand in je richting botsen, een extra impuls en worden daardoor energierijker. Je neemt dat waar als traagheid. Als je de bol weer afremt tot stilstand, staan de fotonen hun extra energie weer af. Het is iets lastiger om rotatie-inertie in te bouwen, maar als de spiegelende bol binnen een oneffen oppervlakte heeft is ook dit mogelijk. Door de bol te laten draaien worden fotonen zo gedwongen in een bepaalde richting (bijvoorbeeld met de klok mee of tegen de klok in) te bewegen. Dit voelt ook als traagheid. Deze energie is ook weer uit de bol te halen door hem tot stilstand te brengen. Trage massa uit licht, dus.

Licht wordt zwaar

De bol lijkt ook zwaar te zijn: tegen je hand te duwen als hij in je hand ligt. De reden is dat licht een roodverschuiving krijgt als het in een zwaartekrachtsveld naar buiten beweegt. De tijd gaat heel iets langzamer naar de aarde toe dan van de aarde af, waardoor fotonen die aan de onderkant van de bol zijn, energierijker lijken dan aan de bovenkant. Door deze (overigens minuscule) blauwverschuiving ontstaat een kracht naar beneden. De bol lijkt (en is dus, natuurkundig gezien) zwaar. Dus we hebben hier niet alleen trage, maar ook zware massa uit licht gemaakt.

Het ontbrekende stukje aan de zwaartekrachtspuzzel

Er ontbreekt nog één stukje aan de puzzel. Hoe oefent de bol zwaartekrachtswerking uit op andere objecten, met andere woorden: hoe vervormt een biljoen kilowattuur aan weerkaatsende lichtenergie binnen een bol ruimtetijd om zich heen, zoals veertig gram materie dat ook doet? Wat denken jullie? Een ding is duidelijk. Hiervoor moeten we echt diep de speculatieve wetenschap induiken…